题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：复制

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：复制

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

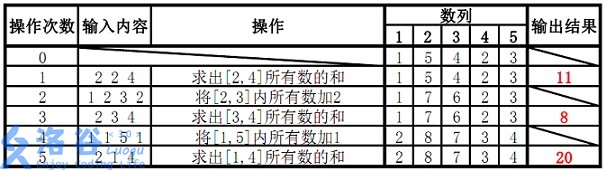
样例说明：

自我感觉良好地重写了一下

对不起 我只会写模板（？）

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include<cstdio>
#include<iostream>
#include<cstring>
#define MAXN 400017
typedef long long LL;
using namespace std;
struct Node{
    LL l, r, lazy, v;
}d[MAXN];
LL n, m;
LL ncnt = 0;
void build(LL i, LL l, LL r){
    if (l > r) return;
    //从一开始 
    d[i].v = 0;
    d[i].lazy = 0;
    d[i].l = l;
    d[i].r = r;
    if (l == r) return;
    LL mid = (l + r) >> 1;
    build((i << 1), l, mid);
    build((i << 1) + 1, mid + 1, r);
 
 
}
 
void pushdown(LL i){
//  cout << "pushdown " << endl;
//  cout << i << ":" << d[i].l << ", " << d[i].r << ": " << d[i].lazy << d[i].v << endl;
    d[i].v += (d[i].r - d[i].l + 1) * d[i].lazy;
//  cout << i << ": " << d[i].v << endl;
    if (d[i].l < d[i].r){
        d[i << 1].lazy += d[i].lazy;
        d[(i << 1) + 1].lazy += d[i].lazy;
    }
    d[i].lazy = 0;
}
 
LL sum(LL i, LL l, LL r){
    if (l > r || d[i].l > r || d[i].r < l) return 0;
//  cout << i << ":" << d[i].l << ", " << d[i].r << endl;
    pushdown(i);
    if (d[i].l >= l && d[i].r <= r) return d[i].v;
    return sum(i << 1, l, r) + sum((i << 1) + 1, l, r);
}
 
void add(LL i, LL l, LL r, LL v){
//  cout << i << ":" << d[i].l << ", " << d[i].r << ": " << d[i].lazy << d[i].v << endl;
    if (d[i].l > r || d[i].r < l) return;
    if (d[i].l >= l && d[i].r <= r){
//      cout << "lazy update" << endl;
        d[i].lazy += v;
        return;
    }
//  cout << "lazy" << endl;
 
    pushdown(i);
//  cout << i << ":" << d[i].l << ", " << d[i].r << ": " << d[i].lazy << d[i].v << endl;
    add(i << 1, l, r, v);
    add((i << 1) + 1, l, r, v);
    pushdown(i << 1);
    pushdown((i << 1) + 1);
    d[i].v = d[i << 1].v + d[(i << 1) + 1].v;
//  cout << i << ":" << d[i].l << ", " << d[i].r << ": " << d[i].lazy << d[i].v << endl;
}
 
int main(){
//  freopen("testdata.in", "r", stdin);
//  freopen("testdata.txt", "w", stdout);
    scanf("%lld%lld", &n, &m);
    memset(d, 0, sizeof(d));
    build(1, 1, n);
    LL x, y, k;
    for (LL i = 1; i <= n; i++){
        scanf("%lld", &x);
        add(1, i, i, x);
//      cout << "? " << endl; 
    }
    LL op;
    while(m--){
        scanf("%lld", &op);
        if (op == 1){
            scanf("%lld%lld%lld", &x, &y, &k);
            add(1, x, y, k);
        }else{
            scanf("%lld%lld", &x, &y);
            printf("%lld\n", sum(1, x, y));
        }
    }
    return 0;
}